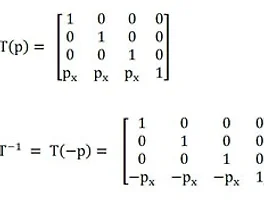- 행렬이란, matrix라고 하며, 행과 열로 이루어진 수의 배열이다.
m x n 행렬은 m행과 n열을 가지고 있다.
때때로 한개의 행이나 열만을 가지는 행렬이 있는데 이를 행 벡터, 열 벡터라고 부른다.
1. 상등
- 동일한 차원을 가지고, 각각의 대응되는 항목이 같은 두 개의 행렬은 같은 것으로 보고 이를 행렬의 상등이라고 한다.
2. 스칼라 곱
- 행렬의 각 항목을 스칼라로 곱하는 방법으로 행렬과 스칼라 곱을 수행할 수 있다.
3. 더하기
- 행렬이 동일한 차원을 가진 경우에는 두 행렬을 더할 수 있다.
4. 행렬의 곱
- 행렬 A가 m x n 행렬이고, 행렬 B가 n x p 행렬일 때, A의 열 수가 B의 행 수가 같으므로 곱이 정의될 수 있다.
- 행렬의 곱에서 가장 중요한 성질은 교환법칙이 성립하지 않는다는 것이다. ( 예외가 있다. )
- 행렬의 곱은 아래와 같이 나타낼 수 있다.
5. 항등 행렬 (Identity Matrix)
- 항등 행렬은 좌 상단부터 우 하단까지의 대각 성분은 1 이고, 나머지 성분은 0인 정방행렬이다.
- 항등행렬의 가장 중요한 성질은 하나의 행렬 A에 항등 행렬을 곱해도 변하지 않는다는 것이다. 말 그대로 항등 행렬이다. (항등원과 역원을 생각하자.)
또한, 항등 행렬은 행렬 곱의 교환 법칙에서 하나의 특별한 예외이다.
6. 역행렬 (Inverse Matrix)
- 항등 행렬에 대해 언급했다. 항등행렬이 항등원이라면, 역행렬은 역원이다.
- 역행렬의 성질
① 정방행렬만 역행렬을 가질 수 있다.
② m x m 행렬 M의 역행렬은 m x m 이며 M-1로 표기한다.
③ 모든 정방행렬이 역행렬을 가지진 않는다.
⑤ 행렬과 역행렬을 곱한것은 항등행렬이다.
- 역행렬은 행렬 방정식 내의 다른 행렬을 풀어낼 때 유용하다.
- 곱의 역에 대한 유용한 특성
7. 행렬의 전치 (Transpose Matrix)
- 행렬의 행과 열의 원소를 교환하면 행렬의 전치를 수행할 수 있다.
'예전 > 3D수학' 카테고리의 다른 글
| [3D 수학] 사원수(Quaternion : 쿼터니언) (4) | 2012.09.12 |
|---|---|
| [3D 수학] D3DXMatrixInverse 의 이해 (0) | 2012.09.05 |
| [3D 수학] 3D 변환 행렬 (0) | 2012.09.03 |
| [3D 수학] D3DX 행렬 (0) | 2012.09.03 |
| [3D 수학] 벡터 (Vector) (0) | 2012.09.03 |