1. 사원수(Quaternion : 쿼터니언)란?
- 3차원 그래픽에서 회전을 표현할 때, 행렬 대신 사용하는 수학적 개념으로 4개의 값으로 이루어진 복소수(Complex Number) 체계이다.
아래 글에선 사원수와 쿼터니언을 번갈아가며 썼다.
(잠깐! 복소수란 현재 교육과정 중 가장 큰 범위의 수로 실수부와 허수부의 합으로 구성된 수이다.)
그렇다면, 사원수를 사용하는 이유는 무엇일까?
- 사원수는 행렬에 비해 연산 속도가 빠르고, 차지하는 메모리의 양도 적으며, 결과의 질에 있어 오류가 날 확률이 적다.
3개의 축에 대한 회전 연산을 동시에 적용하는 경우에 행렬을 사용하면 한 축이 소실되는 김벌락 현상이 발행할 수 있는데, 사원수를 사용하면 이 현상을 막을 수 있다. (미리 말해두지만, 사실 이것도 완벽하기 막지는 못한다.)
2. 사원수의 정의
- 사원수는 4차원 복소수 공간(Complex Space)의 벡터로서 다음과 같이 나타낸다.
- 사원수를 q = s + v 형태로 쓰기도 하는데, 여기서 s 는 q의 w 성분에 해당하는 스칼라(Scalar) 값이고, v는 q의 x, y, z 성분에 해당하는 벡터(Vector) 부분이다.
3. 사원수의 특징
- 사원수의 곱은 일반적인 분배법칙을 따르며 허수 성분인 i, j, k는 다음과 같은 특징을 갖는다.
(필자의 생각)
여기서 i, j, k 는 각각 x, y, z축에 대비된다고 할 수 있다. 정확히 그 축을 말하는 것이 아니라 어떠한 물체의 3축이라는 것이다. 따라서 서로 직교 하므로 ij와 ji는 교환법칙이 성립하지 않고, 역수 관계인 것이다.
또한, 서로 외적하면 다른 축을 가리킨다. 때문에 각각의 축에 대비된다고 할 수 있다.
위와 같은 두 사원수 q1,q2가 있을 때, 두 사원수의 곱q1q2는 다음과 같다.
사원수를 스칼라, 벡터 형태로 표기할 때,
이렇게 표현할 수 있고, 두 사원수의 곱은 다음과 같다.
이는 앞에서 나온 q1,q2의 곱의 부호를 제외하고 곱했을 때 나온 값과 같다.
- 사원수는 켤레(Conjugate)를 갖는다.
- 사원수의 역수
그리고 아래와 같은 특징을 갖는다.
- 단위 쿼터니언을 갖는다.
q = [1, (0, 0, 0)]
단위 쿼터니언은 3D 공간에서 오일러, Axis 대신 방향을 표현한다.
쿼터니언으로 방향을 표현하려면 쿼터니언을 행렬로 변환하거나, 행렬을 쿼터니언으로 변환하는 방법이 필요하다.
3. 사원수의 회전
- 축 A에 대한 각도 Θ 만큼의 회전을 사원수로 나타내면,이다.
(이것에 대한 증명 과정은 추후 업로드 할까말까...ㅠㅜ)
이 사원수로 점 P를 회전하려면 qPq-1을 하면된다.
최종적으로 얻어진 사원수를 행렬로 변환하면, 아래와 같다.
4. 사원수의 보간
- 보간(interpolation)이란 처음과 끝의 값을 가지고 중간에 잇는 값을 계산해 내는 것이다.
물체의 애니메이션을 수행할 때, 보간을 통해 계산된 키프레임 사이의 중간 방향을 생성한다.
이런 사원수는 정규화 해줘야 한다. 이 함수 q(t)는 q1과 q2사이의 호를 따라간다.

여기에서 구면 선형보간(spherical linear interpolation : slerp)이 나타났다.
일단 유도과정은 생략하고 보면 다음과 같다.
쿼터니언에서 제일 중요한 것은 회전으로 이로 김벌락을 피하는 것이다.
이에 대해선 추후 업데이트 ... 하겠다.
'예전 > 3D수학' 카테고리의 다른 글
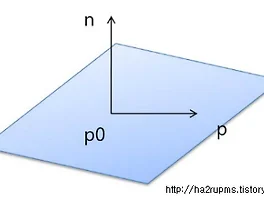
| [3D 수학] 평면 (1) | 2012.09.14 |
|---|---|
| [3D 수학] D3DXMatrixInverse 의 이해 (0) | 2012.09.05 |
| [3D 수학] 3D 변환 행렬 (0) | 2012.09.03 |
| [3D 수학] D3DX 행렬 (0) | 2012.09.03 |
| [3D 수학] 기본적인 행렬 (0) | 2012.09.03 |