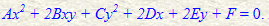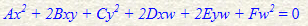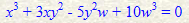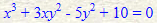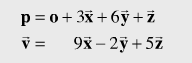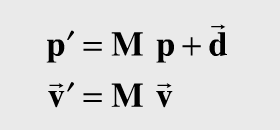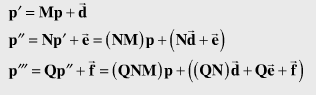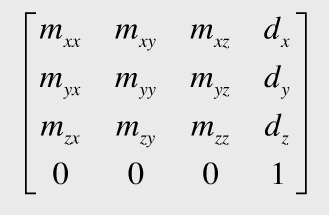http://www.silverwolf.co.kr/73432
실세계의 한점 Q = (X, Y, Z)는 3차원의 점이다
이 점이 앞시간에서 배웠던 투영 스크린 상의 한 점 (X, Y)로 2차원 점으로
변환되는 관계를 투영 변환이라 한다.
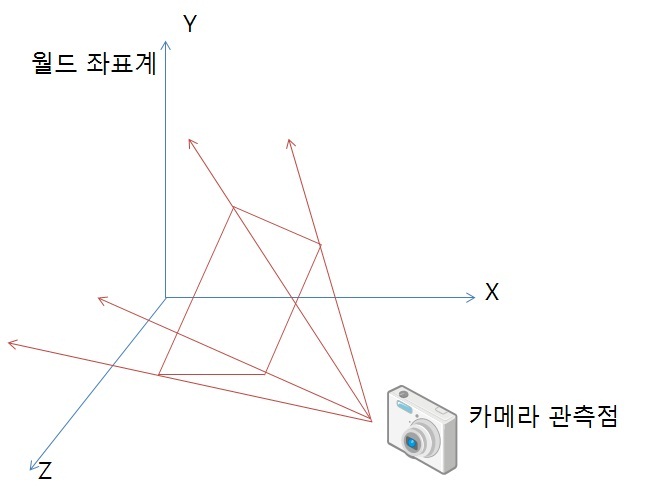
이렇게 투영변환을 사용할 때는 동차 좌표계라고 알려진 좌표계를 사용하는게 편하다.
그럼 동차좌표계가 그럼 무엇인가요?
3D에서는 기본적으로 3차원좌표계이지만 이것을 어떤 목적으로 4차원으로도 확장이 가능하다.
이렇게 어떤목적을 위하여 한 차원의 좌표(n) 을 한차원 추가된 좌표 (n+1)로 표현을 하는 것을 동차 좌표계라 한다.
예를 들자면
3차원 좌표 (x, y, z)는
4차원 좌표 (x, y, z, w)형태로 표현 한다는 것이다.
기본적인 성분 x y z 에 w가 추가된것으로 3D 상에서는 x/w y/w z/w로 나타낸다.
투영행렬에서 동차좌표를 사용하는 이유가 무엇인가요?
시점으로 보이는 점들의 위치가 중요한게 아니라 시점으로 부터 방향이 중요하기 때문이다.
그림을 보자
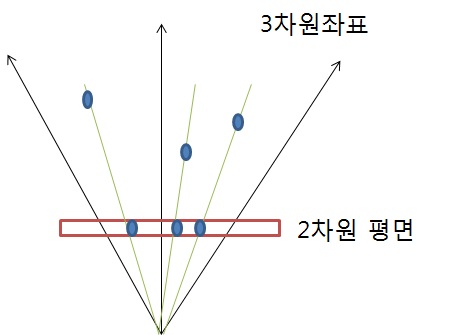
투영행렬에 대한 이론을 간략히 설명한 것이다.
우리가 원하는 것은 3차원의 점들이
2차원 평면인 빨간 네모안에 다 모인다는 것이다.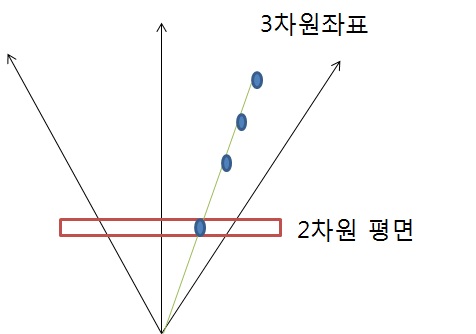
다음 그림은 점들의 위치가 서로 다른 3차원 점이 2차원에 투영되는 점은 결국 하나가 되버린다느는 것이다.
그래서 시점으로부터 방향이 중요한 것이 무엇인지 이해할 수 있다.
3D에서도 동차좌표를 사용하던데 ?
동차좌표계가 있음으로 오브젝트의 이동을 행렬간의 곱셈으로 표현이 가능하다.
이동, 크기, 회전을 모두 담은 행렬은 최소 4X4 행렬일 수 밖에 없다.
이 행렬과 정산적인 연산을 하기 위해서는 벡터도 행렬이므로 1X4 또는 4X1의 행렬 형태를 맞춰야한드는 것이다.
포인트(w=1)과 벡터(w=0)을 가늠할 수 있는 기준이 되기도 한다.
동차좌표는 방향과 점의 구분시켜준다.
x,y,z의 3차원 좌표계 구조체는 이게 점인지 방향인지 구분이 모호하다.
그래서 동차 좌표계가 포함된 4차원 좌표계로 표현하면 (0은방향 1은 위치)로 표현할 수 있다.
0은 방향을 의미하는 벡터로
위치,방향으로서 서로 다른 벡터인지 구분이 가능
(방향벡터가 방향이 같고 위치가 다르다라는 것은 확대 또는 축소인 상태)
1은 위치를 의미하는 벡터로
위치가 서로 다른 벡터인지 구분이 가능
0의 동차항을 가지는 벡터는 확대, 축소, 방향변경이 가능하다.
1의 동차항을 가지고 있는 벡터는 이동(위치변화)가 가능하다.
0의 동차를 가지는 벡터는 1~3행
1의 동차항을 가지는 벡터는 4행
그럼 동차좌표계를 어떻게 구하는 가요?
동차좌표계 상 변환된 좌표 = p * 월드행렬 * 뷰행렬 * 투영행렬
투영행렬에서 카메라공간상에 존재하는 점과 카메라 위치사이의 깊이 z를 최종 결과점 x y z 에 각각 곱해지고 w에 저장되는데 바로 이 과정이 동차좌표계를 위한 과정이다.
해당 좌표공간(카메라 공간, 투영공간, 월드 공간)에서 3D 좌표를 얻어내려면 w로 나눠댄면 된다.
여기서 월드공간과 카메라공간에서는 w값이 항상 1이기 때문에 변화가 없지만
투영공간에서는 w값이 카메라 공간에서의 카마레위치에서 부터 정점사이 거리이기 때문에 z값에 따라 정점의 위치와 크기가 변환되는 것임을 짐작할 수 있다.
그럼 우리가 사용하는 이미지카메라 모델의 경우?
영상 평면이 투영공간이 되고 이는 2차원 평면이다.
때문에 동차 좌표는 q = (q1, q2, q3)로 표현할 수 있다.
투영공간에서 비례하는 점은 모두 동일 하므로 q1과 q2를 q3로 나누어 줌으로 써 실제 2차원 픽셀 좌표를 얻을 수 있다.
동차 좌표계를 사용하면 fx fy cx cy 등의 카메라 파라메터를 3X3 크기의 행렬 하나로 표현 할 수 있다.
우리는 이 행렬을 카메라 내부행렬이라 부른다.
카메라 내부행렬을 표현하는 방법은 Heikkila 와 Silven의 논문을 참고해보면된다.
(A Four-step Camera Calibration Procedure with Implicit Image Correction)
이제 실세계의 한점이 카마레라로 투영되는 관계는
다음과 같은 간단한 행렬 연산으로 표현이 가능하다.
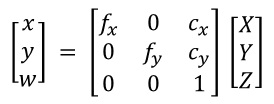
위행렬을 실제로 곱해보면 w = Z가 되고
점 q는 동차 좌표계로 표현되어 있기 때문에 x와 y좌표값을 Z로 나누어야 원래 좌표를 얻을 수 있따.
그럼 OpenCV에서는 이를 제공해주는 함수는 없나요?
일반 좌표계를 동차 좌표계로 변환하는 cvConvertPointsHomogenious() 함수를 제공하고 있다.
void cvConvertPointsHomogenious(const CvMat* src, CvMat* dst)
일반좌표계를 동차 좌표계로 서로 호환이 가능하다.
입력 Scr 과 dst 의 행렬 차수가 서로 같은 경우 내부 데이터는 단순히 복사되며
행렬차수가 Scr > dst 이면
dst행렬의 원소들은 src 행렬에 저장된 벡터의 맨 마지막 원소로 나머지 원소값들을 나누어 계산된다.
행렬차수가 scr < dst 이면
점들이 모두 복사되면서 dst배려에 있는 모든 벡터의 마지막 원소에 1이 추가된다.
Homogeneous Coordinates(동차좌표계)
p.s 퍼가시는 분이 있어서 약간 수정했습니다^^
-동차좌표계란?
3D에서는 기본적으로 3차원좌표계이지만 어떤 목적에 의해 4차원으로 확장할 수 있는데, 이것이 동차좌표계다. 기본적인 성분 x, y, z에 w가 추가된 것으로 3D상에서는 x/w, y/w, z/w로 나타낸다. 동차좌표계가 있음으로 오브젝트의 이동을 행렬간 곱셈으로 표현할 수도 있으며, 포인트(w=1)와 벡터(w=0)를 가늠할 수 있는 기준이 되기도 한다.
-동차좌표계와 투형행렬
투영행렬에서, 카메라공간상에 존재하는 점과 카메라 위치 사이의 깊이값(z)를 최종 결과점의 x, y, z에 각각 곱해지고, w에 저장되는데 바로 이 과정이 동차좌표계를 위한 과정이다. 해당 좌표공간(카메라공간, 투영공간, 월드공간 등등)에서의 3D좌표를 얻어내려면 w로 나눠내면 된다. 여기서 월드공간, 카메라공간에서는 w값이 항상 1이기 때문에 아무런 변화가 없지만, 투영공간에서는 w값이 카메라공간에서의 카메라의 위치에서부터 정점사이의 거리이기 때문에 z값에 따라 정점의 위치와 크기가 변환되는 것임을 짐작할 수 있다. 따라서, 셰이더에서 다른 공간은 별로 상관없지만, 투영공간상에 존재하는 좌표를 다룰 경우 동차좌표계상에 존재하기 때문에 w성분으로 나누어 줘야한다.
[푸의 요약]
라이푸의 큐티한 그림을 보자면-_- 별은 카메라, 파란선은 전방 후방 클립면, 검은색네모는 버텍스이다. 만약 우리가 삼각형을 그
리기위해서 버텍스를 입력하게되면 w=1 이다. 이것이 버텍스셰이더를 거치게되면서 w값이 변경된다. 정확히 말하면 프로젝션매트릭스를 거치기전까지 w=1을 유지한다. 프로젝션을 거치게되면(버텍스셰이더를거치게되면) 현재 카메라좌표와 버텍스간의 거리값이(깊이값) w에 저장하게 되고 x,y,z에도 곱해진다. 이런 역할을 하는 것이바로 동차좌표계이다. w=1이라는 규약은 전후방 클립면의 총거리를 1로 나타내는 것이다. 그렇다면 동차 좌표계를 실제로 사용되는 곳이 어딜까? 셀프셰도우 구현시 DepthMap을 렌더타겟에 그리게 되는데 이때 버텍스셰이더에서 mal(vPOS, mWVP) 정보를 픽셀셰이더에서 이를 vPos.xyz / vPos.w로 나누어 3D상에서 실제좌표를(Z깊이값) 얻어 낼때 사용된다. 더 정확하게 말하면 버텍스셰이더에서 Z값이 아닌 픽셀셰이더를 거쳐 선형보간된 Z값을 얻을 때 사용되는 것이다. 그리고 디퍼드 구현때도 G-Buufer에서 Original View Position을 픽셀셰이더에서 재건할때도 동일한 원리를 적용하여 vPos.xyz / vPos.w값을 사용하게 된다.
http://neosafe.blog.me/130044604300
http://ekessy.tistory.com/2
동차 표현 vs 동차 좌표계
4차원 벡터 (x,y,z,w)에서 w가 1이 아닌 값을 1이 되도록 나누어 주는 이런 표현이 모두 동차 좌표계라고 알고 있는 사람들이 많은데 그것은 잘못된 지식이다.
동차 표현에 대해서
접어두기..
따라서 위치에 대한 정보를 나타낼 수 없다.
하지만 가상의 3D 세계란 위치를 가지고 있는 객체들을 표현할 수 있어야 한다.
그래서 나온 것이 아핀 공간이다.
아핀 공간은 벡터 공간 + 점 공간이라고 생각하면 된다.
이 공간에서는 벡터 공간에서 존재하지 않는 몇 가지 연산자가 추가되는데
1. 벡터 + 점 = 점
2. 점 - 점 = 벡터
이 두 가지 연산이다.
하지만 3차원 공간에서 벡터를 표현하는 방식은 ( x, y, z )이고 마찬가지로 점을 표현하는 방식도 ( x, y, z )이다.
서로 다른 두 엔티티를 구별할 수 있는 방법이 없어서 도입된 것이 바로 동차 표현이다. 점은 ( x, y, z, 1 ), 벡터는 ( x, y, z, 0 ) 이렇게 말이다.
이 형식대로 위의 연산을 해보면 벡터 + 점은 당연히 w가 1이 되므로 점이 되는 것이 자명하고 마찬가지로 점 - 점도 w가 0이 되므로 벡터가 되는 것이 자명하다.
접어두기..
동차 좌표계에 대해서
접어두기..
사영 기하 공간은 무한 원점에서 모든 선분들이 교차를 하기 때문에 우리가 사용하는 일반적인 데카르트 좌표계를 사용해서 해석적인 방법으로 좌표를 표현할 수 없다.
이후에 수학자들이 w=1인 초평면이 3차원 공간을 나타낸다는 것을 알아냈고 이제 동차 좌표계를 사용해서 사영 공간에서도 해석적인 좌표를 표현할 수 있게 되었다.
접어두기..
Projective transform(투영변환)
실세계의 한점 Q={X, Y, Z}이 투영스크린 상의 한점 (X, Y)로 변환되는 관계를 Projective transform(투영변환)이라고 한다.
Homogeneous coordinates(동차 좌표계)
어떤 목적에 따라 N차원에서 1차원 추가된 N+1차원으로 표현하는것을 Homogeneous coordinates(동차 좌표계)라고한다.
동차좌표계의 경우 N차원의 투영공간에 존재하는 점을 동촤좌표계로 표현하면 N+1차원의 백터로 표현된다.
Ex) (X, Y, Z)좌표는 (X, Y, Z, W)형태로 표현된다.
Homogeneous coordinates(동차 좌표계)로 표현된 두점의 각 좌표값이 서로 비례할 경우, 이 두점은 동일한점으로 취급된다.
3D에서의 필요한 벡터는 기본적으로 3차원좌표계이다.
이것을 4차원 좌표계로 확장하는데 추가되는 개념이 바로 동차 좌표계이다.
동차좌표는 결국은 4x4 행렬과의 연산 때문에 필요하다.
이동,크기,회전을 모두 담은 행렬은 최소 4x4 행렬일 수밖에 없다.
이 행렬과 정상적인 연산을 하기 위해서는 '벡터도 행렬' 이므로 1x4 또는 4x1형태를 맞춰줘야 한다.
그렇다면 처음부터 끝까지 동차좌표계가 1이면 된다.
게다가 당연히 1이라는 표시만 해주면 되는 기호는 생략 가능한데 굳이 따라다니는 아래와같다.
동차좌표는 방향과 점의 구분시켜준다.
x,y,z(DirextX는 D3DXVECTOR3)의 형태의 3차원 좌표계 구조체는 이게 점인지 방향인지 구분이 모호하기 때문에 동차 좌표계가 포함된 4차원좌표계로 표시하게 되면(0은 방향,1은 위치) 좀 더 그 의미가 확실해진다.
┌ 1 , 0 , 0 , 0 ┐ - x축 벡터
│ 0 , 1 , 0 , 0 │ - y축 벡터
│ 0 , 0 , 1 , 0 │ - z축 벡터
└ 0 , 0 , 0 , 1 ┘ - 이동관련 벡터
각 4개의 동차좌표계를 포함한 벡터(1x4행렬)에서 각 벡터의 동차항은 0,1로 이루어져있다.
0은 방향을 의미하는 벡터로써 위치,방향으로서 서로 다른 벡터인지 구분 가능하다.
(방향벡터가 방향이 같고 위치가 다르다라는 것은 확대 또는 축소인 상태이다.)
1은 위치를 의미하는 벡터로써 위치가 서로 다른 벡터인지 구분가능하다.
그러므로,
0의 동차항을 가지고 있는 벡터는 확대,축소(크기변화),방향변경(방향변화) 가능하고
1의 동차항을 가지고 있는 벡터는 이동(위치변화)가 가능하다.
0의 동차항을 가지고 있는 벡터 1행~3행, 1의 동차항을 가지고 있는 벡터 4행
결국 동차좌표계가 0이면 방향변화,크기변화라고 표현 할 수 있지만 위치변화라고는 말할 수 없다.
동차좌표계가 1이면 위치변화 라고 표현할 수 있지만 방향이나 크기변화라고는 말할 수 없다.
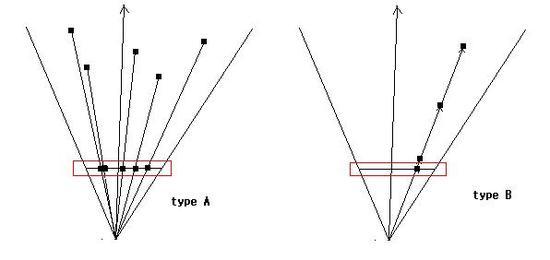
동차좌표는 투영행렬과의 연산에서 특별한 의미를 가진다.
투영행렬은 3D차원의 공간을 2차원의 공간으로 변환시킨다.
그 과정에서 시점으로부터 보이는 점(vector)들의 위치가 중요한게 아니라 결국 시점으로부터의 방향이 중요하다게 된다.
type A는 투영행렬에 대한 이론을 간략하게 설명해 놓은 그림인데 우리가 결국 원하는 것은 3차원의 점들이 2차원인 빨간상자안에 모인 위치들인 것이다.
type B는 점들의 위치보다는 시점으로부터의 방향이 중요한 것이 무슨 말인지 이해하기 위한 그림이다.
위치가 서로 다른 3차원상의 점(vector) A(5,5,?), B(10,10,?), C(100,100,?)이라 생각해 보면 2차원에 투영되는 위치는 결국 하나가 되버린다.
(*z좌표를 ?로 표시한 이유는 정확한 수치로 넣을 경우 오해 소지가 생길 수도 있기 때문이다.)
DirextX기준으로 투영행렬의 마지막에는 카메라 행렬까지 반영한 z값을 가지고 3차원좌표 (a/z,b/z,c/z)의 형태를 가지게 되는데 이 과정을 (a,b,c,z)이렇게 대신함으로써 (a/z,b/z,c/z,1)로 마무리하게 하고 있다.
예를 들어 A의 동차 좌표계가 5이라면 B는 10, C는 100일 것이고 결국은 A,B,C는 같은 2차원 좌표인 (1,1)이라는 픽셀에 찍힐 것이다.
동차좌표라는 것은 마치 '지도의 축소비율'처럼 축소나 확대에 관한 비례개념처럼 보여지기도 하고 이 좌표가 1이 되서 완전한 위치의 형태(변환 끝)로 변형되었는지도 의미하게 된다.
| 동차좌표계 질문 | 올려짐: 2009-05-22 02:10  | ||||||
| 동차 좌표계에 대한 어설픈 이해를 하고 있는데요 이해가 안되는부분이 있어서요 x y z w 에서 w로 나누어 주어야 우리가 원하는 좌표계로 나온다는것은 알겠는데 그렇다면 x y z w 는 어디 좌표계에 존재하는건가요? w가 1이 아닌 값이 나와서 나누어준다는것인거 같은데 그렇다면 어떨때 다른 값들이 들어오는지 알고 싶어요... [엉뚱한 질문일수도 있는데 도저히 이해가 안되서..]
| |||||||
동차좌표 (Homogeneous Coordinates)
OpenGL에서의 동차좌표계는 4x4의 3차원 좌표 행렬을 4개의 수로 줄인 것입니다.
실제로 OpenGL에서는 4차원으로 연산이 이루어지는데 바로,
(x, y, z, w)
- x : x좌표
- y : y좌표
- z : z좌표 (우리가 흔히들 아는)
- w : 점인지 선인지 표현 (0은 벡터, 1은 점)
의 요소로 이루어진 동차좌표계를 사용합니다.
3개의 좌표만으로는 점인지 선인지 알 수 없기 때문에 네번째 요소인 w를 사용하여 4차원으로 구별합니다.
이 동차좌표계는 3차원의 모든 상황들을 표현할 수 있습니다.
1차원 점 : (x, 0, 0, 1)
2차원 점 : (x, y, 0, 1)
3차원 벡터 : (x, y, z, 0)
이런 식으로 표현할 수 있습니다.
동차좌표를 사용하는 이유는 시점으로부터 방향이 중요하기 때문입니다.
- OpenGL에서 표현되는 공간은 우리 눈에 보이지 않더라도 앞과 뒤의 구분이 있다는 것입니다. 그렇기 때문에 점과 벡터의 구분이 필요합니다. -> 동차좌표계 사용
- 동차좌표계가 있음으로 오브젝트의 이동을 행렬간의 곱셈으로 표현할 수 있습니다.
- 제가 써놓고도 읽으시는 분들이 헷갈리실 수 있겠다는 생각이 드네요...
컴퓨터 그래픽스에서는 동차좌표의 마지막 요소를 Scale Factor로 사용할 수 있으며, 만약 어떤 점의 좌표를 (x, y, z, w)로 표현했다면 실제 3차원 좌표의 값은 (x/w, y/w, z/w)로 될 수 있습니다.
동차좌표계를 이용한 이동, 회전, 크기변환
이동변환
크기변환
회전변환
- x축 회전
- y축 회전
- z축 회전
위 그림에서 점 P는 벡터 OP로 표현됨(1).
마찬가지로 점 Q는 벡터 OQ로 표현됨(2).
따라서 벡터 PQ는 벡터 OQ-OP 임(3).
그리고 점 Q는 벡터 OP+PQ로도 표현됨(4).
(1) ~ (4)를 수식으로 표현하면 아래와 같음.
식 (3)에서 정의된 벡터 PQ는 크기와 방향만 나타내므로 공간상의 어디에 있든 동일함.
반면 식 (4)에서 정의된 점 Q는 점 O를 기준으로 정의된 점 P에 의해 규정되어짐.
식 (3), (4)는 점 P를 제외하면 동일한 식이지만 벡터 표현이냐 점 표현이냐에 따라 2개의 식으로 구분하여 표현하여야 하는 번거로움이 있음.
따라서 아래와 같이 두 식을 변형하여 작성 할 수 있음.
각 항의 계수만으로 다시 표현하면 벡터는 (a, b, c, 0), 점은 (a, b, c, 1)로 표현할 수 있음.
이러한 표현을 동차좌표 표현(Homogeneous Coordinates Representation)이라 함.
컴퓨터 그래픽스에서는 동차좌표의 마지막 요소를 스케일 펙터(Scale fector)로 사용할 수 있으며,
만약 어떤 점의 좌표를 (x, y, z, w)라고 표현하였다면 실제 3차원 좌표의 값은 (x/w, y/w, z/w)가 됨.
동차 변환 표현(Homogeneous Transformation Representation)은 아래와 같음.
같은 동차 표현으로 생각한다면 Rotation 파트는 벡터 표현이고 Position 파트가 점 표현임을 쉽게 알 수 있음.
P.S.
Robotics관련 서적에서 뭔가 부족했던 2%가 채워졌음. ㅋㅋㅋㅋㅋ
Homogeneous Coordinates
변환을 행렬로 표현하여, 변환된 점P'을 변환전의 점P와 변환행렬의 곱으로 표현하는 것이 속도면에서나 다루는 면에서 아주 장점을 많이 가지고 있다. 앞 일지에서 변환에 대해서 소개를 했는데 이번 일지에서 변환을 어떻게 행렬로 표시할 수 있으며, 이때 필요한 수학적 magic인 Homogeneous Coordinates에 대해서 알아 보기로 합니다.
하지만......여러 자료를 살펴 보았지만 그 근저에 흐르는 수학적 의미는 잘 이해되지 않더군요. 또는 물리적 의미또한 말이죠.
혹 더 궁금하신 분은 이 자료를 참고하세요...
blkinn-pipeline.pdf
먼저 동차좌표계(Homogeneous Coordinates)에 대해서 알아 봅니다.
주된 출처는 : http://www.cs.mtu.edu/~shene/COURSES/cs3621/NOTES/geometry/homo-coor.html
17.1. Homogeneous Coordinates
17.1.1. 동차좌표의 의미
동차좌표계를 사용하는 이유중의 하나는 바로 무한대(infinity) 개념을 활용할 수 있다는 것이다. 유클리트 좌표계에서는 무한대는 존재하지 않는 거죠. 수학자들이 생각하기에 무한대(∞)의 개념을 사용할 수 있다면 많은 기하학적 개념과 계산이 아주 쉽게 이루어진다고 생각합니다. 이는 곡선과 표면 디자인의 경우에 명확해진다고 하네요. 동차좌표계를 사용하지 않고는 컴퓨터 그래픽과 CAD 분야에서 커브와 곡면 표현이 아주 어려워집니다.
두 실수 a, w 가 있다고 생각해보자. 그리고 a/w 값도 계산해보자. 만약 a를 고정시키고 w값을 변화시키는데, w를 계속 작게 만들어 주면 a/w 값은 계속 커질 것이다. 만약 w가 제로에 가까워지면 a/w는 무한에 가까워진다. 그러므로 무한대의 개념을 사용하기 위해서는 두 수가 필요하고 이 두 수를 나눈 값(v) (v=a/w) 역시 필요하다. 만약 w가 0이 아니라면 v는 정확하게 a/w가 된다. 만약 w가 0이라면 무한대의 값을 (a, 0) 처럼 정의하면 된다. 그러므로 무한대의 개념이 한 쌍의 숫자 (a , w) 혹은 분수 a/w로 표현가능하다.
자...이제 이것을 xy평면에 적용해보자. 만약 x 와 y 대신에 각각 x/w , y/w 이렇게 치환하면, 함수 f(x,y) = 0 은 f(x/w, y/w) = 0이 된다. 만약 함수 f(x,y)가 다항식이라면, 함수 f(x/w, y/w)는 다항식에 w의 n제곱을 곱해주면 계수가 다 정리가 된다. 여기서 n은 다항식의 차수이다.
예를 들면, 하나의 직선 Ax + By + C = 0 이 있다고 하면, x 대신에 x/w, y 대신에 y/w를 치환하면 직선 A(x/w) + B(y/w) + C = 0 이 된다. 이 식의 양변에 w를 곱해주면,
Ax + By + Cw = 0
이 된다.
이제 2차 다항식을 예를 들면,
역시나 치환해주고 w제곱으로 곱해주면,
위의 두 다항식을 주의깊게 보면 각 항의 차수가 모두 같다. 즉 균일하다! ! ! Homogeneous하다! ! ! 이래서 동차좌표계라고 합니다......
직선의 식 경우에, x, y, w 항의 차수가 1이고 그 다음 2차 다항식의 경우에는 모든 항(예: x제곱, xy곱, y제곱 ,yw곱, w제곱)이 2차이다.
만약 n차 다항식이 있을 경우, w를 도입하고 나면 모든 항의 차수가 n차가 된다. 결과적으로 이러한 다항식은 차수가 동일한 다항식 즉, homogeneous polynomials이라고 하고 좌표계 (x,y,w)를 homogeneous coordinate라 한다.
그러니까 Homogeneous라는 말은 말그대로 다 동일하게 만들어져 있다는 의미이다.
풀어쓰면, 직교좌표계(x,y)에서 직선의 1차 다항식은 x에 대해서 1차, y에 대해서 1차이지만 상수는 0차가 된다. 그에 반해 Homogeneous 좌표계(x,y,w)에서는 직선의 1차 다항식이 모두 x , y, w에 대해서 1차가 된다. 그래서 균일하다는 말을 할 수 있다.
등차좌표계에서 n차 다항식이 있으면, w의 n제곱으로 나누어 주고, x와y를 각각 x/w와 y/w로 치환하면 직교좌표계의 n차 다항식이 된다. 예를 들면.....
수정(2014.10.6) : 곰튕이님의 지적대로 실수가 있네요. x와y를 각각 x/w와 y/w로 치환하면을 x/w와 y/w를 x와y로 치환하면으로 바꾸어야 합니다.
이라면.....
이것은 3차원에서도 그대로 적용된다.
17.1.2. 중요한 점
동차좌표계에서 한 점(x, y, w)가 있다면, xy평면에서 해당하는 점은 무엇일까? 이것은 위에서 언급한 것을 생각하면 쉽게 (x/w, y/w)가 됨을 알 수 있다. 따라서 동차좌표계에서 한 점(3, 4, 5)은 xy평면에서는 (3/5, 4/5) 즉 (0.6, 08)이 된다. 같은 식으로 동차좌표계에서 한 점 (x, y, z, w)은 실공간에서 (x/w, y/w, z/w)이 된다.
그럼 반대로 xy평면에서 한 점 (x, y)에 대한 동차좌표는 무얼까? 그건 단순히 (x, y, 1)이다. 즉 w 요소를 1로 두면 된다. 그런데 이건 맞기는 하지만 전부를 말하는 것은 아니다. 왜냐면 답이 하나가 아니기 때문이다. 답은 다음과 같다.
xy평면에서 한 점(x,y)에 대한 동차좌표는 (xw, yw, w)가 된다. 여기서 w는 0이 아니다. 따라서 동차좌표로 단 한 점으로 변환되지 않는다. 꼭 기억하세요.
17.1.4. 무한대
도입부에서 언급했듯이 동차좌표계는 무한대를 잘 표현한다. 한 점(x, y)에 대해서 동차좌표로 다음과 같이 1/w를 곱하여 전환하면...
(x/w, y/w, 1/w). 이때 w가 0에 가까워지면 (x/w, y/w)는 (x, y)방향으로 점점 커지고 멀어진다. 만약 w가 0이 되면 무한대가 된다. 그러므로 동차좌표 (x, y, 0)는 (x, y)방향의 무한대라고 말할 수 있다.
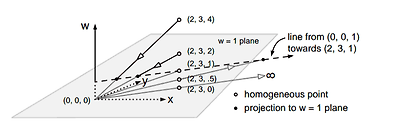
이를 그림으로 표현해 본다면.....만약 동차좌표 (2, 3, w)가 있다고 하자. w값을 점점 작게 해서 xyw좌표계에 표시하면....아래와 같이 된다.
위의 그림에서 보면 w값이 4, 2, 1, 0.5, 0일때의 점을 표현해놓았다. w가 0에 접근함에 따라 원점에서 (2, 3)방향으로 멀어짐을 알 수 있다. w = 0 인 경우 그 점은 사실 위치가 없는 벡터로 취급할 수 있다. 이 부분은 아래 점과 벡터에서 다시 다루어질것이다.
사실 이 개념 즉 어떤 방향으로의 무한점은 곡선과 곡면을 표현할 때 중요하게 사용된다.
만약 좀 더 수학적 설명을 원하시면 아래를 참고하세요....
9781852338015-c1.pdf
http://cyhome.cyworld.com/?home_id=a1746487&postSeq=3131658
17.2. Points와 Vectors 출처 : http://www.docstoc.com/docs/42422791/2-Geometry-Homogeneous-Coordinates
이제 약간 수학적인 내용일 수도 있습니다. 하지만 사실 위의 동차좌표가 컴퓨터 그래픽에 도입된 배경에 해당하는 내용이어서 하지 않을 수 없네요.....여기서는 점과 벡터의 치이와 그리고 그 표현에 있어서의 차이에 대해서 알아 봅니다.
3차원 공간에서 점과 벡터를 나타내기 위해서는 세개의 숫자가 필요합니다. 그래서 이 둘을 같은 것으로 생각하기 쉽죠. 하지만 완전 다른 겁니다. 왜냐면 계산하는 방법도 다를뿐더러 행동도 다르니까요.
그럼 볼까요.....
먼저 일차원에서 시간에 관한 계산을 예를 들어 보죠.
17.2.1 1차원에서의 시간 계산
시간 표현에서는 2가지가 존재합니다. 하나는 시간의 어떤 지점(예, 수업이 2시에 있다) 나머지 하나는 시간의 경과(수업이 2시간짜리다)입니다. 그럼 이 지점과 경과에 관한 연산을 볼까요.
- 2시 수업 + 3시 수업 ≠ 5시 수업
- 2시간 짜리 수업 + 3시간 짜리 수업 = 5시간 짜리 수업
- 수업이 5시에 끝남 - 2시에 시작함 = 3시간 짜리 수업
- 3시 수업 두개 ≠ 6시 수업 하나
- 수업 두개가 3시간 짜리 = 6시간 수업
- 3시간짜리 수업이 5시에 시작 = 8시에 끝나는 수업
- 2시에 시작하고 10시에 끝나는 수업, 수업은 6시에 반이 진행됨. 1/2(2시) + 1/2(10시) = 6시
시간에 대한 좌표를 설정한다고 생각하면....사실 시간의 어떤 지점을 표현하기 위해서는 동경을 기준으로한 표준시로 하죠. 관찰자의 위치에 따라 시간은 달라질 수 있죠. 서울이 아침 6시면 LA는 오후 10시......하지만 이런 좌표의 차이와 상관없이 시간의 경과는 관찰자의 위치와 무관하죠. 즉 서울에서 2시간 경과되는 것과 LA에서 2시간 지나는 것은 같은거죠.
17.2.2. 기하학적 유사성
위의 시간에 대한 설명(즉, 시간과 시간경과는 다르다는 것.....)을 기하학에서 도입하면.....
Point는 공간의 어떤 위치를 표현하는 것이고 Vector는 공간에서의 이동(displacement)를 표현하는 것이다. 조금 구체적으로 설명하면...
Point : 점들을 빼는 것으로 벡터를 하나 만들 수 있다. 위의 시간개념에서 보면 3번째 연산1이다. 그리고 점에 가중치를 두어 계산하여 또 다른 점을 구할 수 있다. 이것은 시간연산에서 마지막 연산2에 해당한다.
Vector : 크기와 방향을 가진다. 벡터는 서로 더하고3 빼고 그리고 스칼라 곱4을 할 수 있다. 벡터에 지점을 더하면 지점(point)을 얻게 된다. 이는 위의 시간연산에서 6번째에 해당한다.
17.2.3. 벡터와 점의 연산
위의 설명을 수식으로 표현하면....주의해서 볼 것은 점과 벡터 연산의 경우이다.
17.2.4 좌표계(Coordinate Frames)
사실 위의 점과 벡터를 정의할 때 좌표계가 지정되어야 합니다. 마치 시간좌표에서 관찰자의 위치를 지정해주어야 하는 것과 같죠.
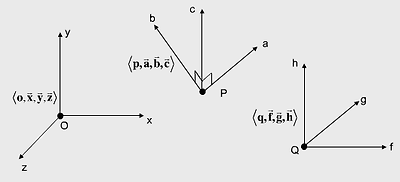
좌표계를 어떻게 정의할 수 있을까요? 쉽게 생각할 수 있는 것은 직교좌표계입니다. 이는 말그대로 축이 서로 직각이 되고 세개의 축은 원점에서 만나죠. 이를 확장하면 서로 수직인 축 세개와 적당한 원점을 정의해주면 좌표계를 정의할 수 있습니다. 아래의 그림에서 보면 세개의 좌표계가 정의되어 있죠. 각각 원점(o ; p ; q)이 다르죠. 그리고 축의 방향(x ; a ; f) 도 다릅니다. 이는 나중에 나올 좌표계 변환에서 사용될 개념입니다.
만약 좌표값으로 (3, 6, 1)과 (9, -2, 3)을 가지고 있다면....그리고 좌표계로 원점O 좌표계를 선택하면 점과 벡터의 경우 다음과 같이 나타낼 수 있습니다.
만약 원점P 좌표계로 표현했으면....다른 결과가 나오겠죠. 즉 같은 좌표값이더라도 좌표계에 따라서 다른 점과 벡터가 됩니다. 즉 좌표값은 좌표계가 없다면 아무 의미가 없죠. 그리고 위의 점과 벡터 표현에서 벡터는 원점이 필요없죠! ! ! ! 오직 축에만 의존하는 물리량입니다. 다시 벡터와 점의 연산이 위의 표현가지고 복기해보면 이해되실겁니다.
음........흐름상 변환을 행렬로 나타낼 수 있다는 내용의 설명이 여기에 추가가 되어야 하는데요.....이미 알고 있다고 하고 넘어갑니다. 기회가 되면 정리하도록 합니다.
다시 본론으로.....이제 점과 벡터의 차이를 알게 되었는데 그럼 도대체 이 차이가 변환에서 어떤 영향을 주는지 볼까요.
17.2.5. 변환 (특히 선형변환)
앞 일지에서 변환이란 점과 점을 대응시키는 함수라고 정의했습니다. 그리고 이 함수를 일반 수식이 아닌 행렬로 표현할 수 있습니다.
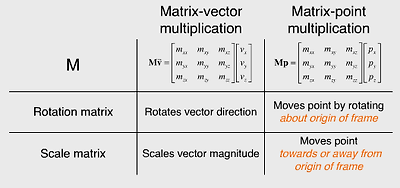
그럼....션형변환시 점과 벡터의 행동양식이 어떻게 다른지 볼까요. 먼저 아래 표를 보면....
위의 표에서 주목해서 볼 것은 바로 주황색으로 된 부분입니다. 이를 그림으로 이해해보면....
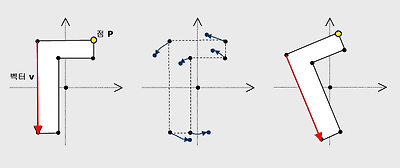
먼저 회전의 경우에...
위의 표에서 벡터의 경우에.....벡터의 방향이 회전하고.....점의 경우에는.....좌표계의 원점을 중심으로 점이 회전한다는 의미를 아실 수 있죠.
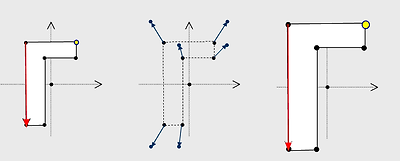
그 다음으로 확대/축소 변환의 경우에는.....
그림에서 보듯이 벡터의 방향은 그대로 유지한 상태에서 그 크기가 변하고.....점의 경우에는 좌표계의 원점에서 멀어지거나 가까워집니다.
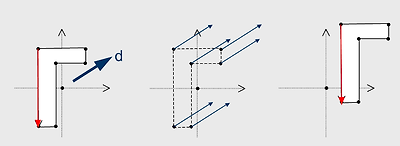
이제 이동변환의 경우를 볼까요.....
그림에서 보다시피 벡터는 하나도 변하지 않습니다. 방향도 그대로 크기도 그대로죠. 하지만 점은 전부 벡터d와의 연산을 통해 바뀌게 됩니다. 기억하시죠. 점과 벡터의 합은 점이 된다는 것을....
자....그럼 이제 정리해볼까요.
즉.....벡터에 대해서는 변환행렬을 곱해주기만 하면 변환후의 벡터를 구할 수 있습니다. 반면에 점의 경우에는 변환행렬과의 곱을 해준 다음...추가로 이동벡터를 더해주어야 합니다.
이처럼....점과 벡터는 변환시 행동이 다르죠....즉 벡터는 선형변환이 되지만....점의 경우에는 선형변환이 되지 않습니다....점의 경우에는 Affine변환입니다.5 수학적으로 말하면 점과 그 변환은 affine공간을 만듭니다. 벡터는 그렇지 않습니다. 이렇듯...점과 벡터이 다르게 행동하면 아주 귀찮죠. 특히나 점에 대해서 변환을 여러개 연속으로 해야 할 경우에는 계산이 아주 복잡합니다. 특히나 역변환을 할 경우에는 더욱 더 어렵게 합니다. 계속 이동벡터d가 따라 붙어서 식이 아주 지저분해지거든요....
위의 사진에서 보듯이 많이 지저분하죠.
이 때........마술이 나타납니다. 바로 Homogeneous Coordinates죠.......
17.3. Homogeneous coordinates의 활용
실용적 의미에서 동차좌표계의 역할은 계산의 편의성과 일관성을 위해서 사용하는 것입니다. 물론 이 포스트의 도입부에서 언급하였듯이 동차좌표계는 단순히 차수를 균일하게 한다는 수학적 의미 외에도 추가적인 수학적 물리학적 의미를 가지고 있습니다. 하지만 모르더라도 활용에는 지장이 없죠. 그리고 다음 일지에서 언급하게될 원근투영(Perspective projection)에서 그 의미를 또 한번 알게 됩니다. 잠간 언급하면.....컴퓨터 그래픽에 동차좌표가 도입된 이유는 사실 원근투영을 하기 위해서라네요...그래서 제가 이걸 공부하고 있구요...저도 원근변환을 해야 하거든요....
17.3.1. 동차좌표를 사용한 점과 벡터의 연산
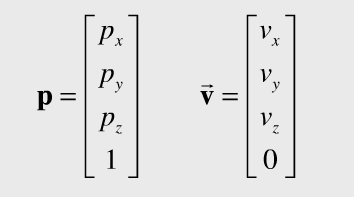
직교좌표에서 동차좌표로의 변환은 직교좌표에서 추가적 요소를 도입하면 되는데....점에 대해서는 1을....벡터에 대해서는 0을 추가합니다.
그리고 3*3 변환행렬과 이동벡터d를 동차표현으로 하면 다음과 같은 4*4 정방행렬이 됩니다.
이제 변환행렬에 점을 곱하건 벡터를 곱하건 동일하게 연산을 처리할 수 있습니다.
음.......하다보니 정작 중요한 것을 놓친 느낌이네요.....잘 모르는 개념을 정리하다보니 좀 허접합니다. 하지만 포스팅전보다는 더 이해의 폭이 넓어졌네요....혹 내용에 오류가 있으면 댓글 주세요...
다음 일지에서는 실용적 내용이 다루어질겁니다....기본기는 이정도로 하고요......음.....원근투영을 다루게 되겠네요...
추가(13.5.25) : 혹 영어가 되시면 특히 리스닝이 하지만 그렇게 어렵지는 않습니다. 근데 하도 고함을 질러서......................이걸 보시면 Homogeneous Coordinates에 대한 물리적 이해가 있을수도....저도 지금 막 검색해서 보고 있는데....뭔가 있을지도 모르겠네요....이 내용을 포스팅할지도...주소는:
처음에는 1차원 공간에 사는 빌과 테드에 관한 얘기...
http://www.youtube.com/watch?v=AyW4Y8APjK4
그러다가 빌과 테드가 같이 움직일 필요가 있어어, 이해는 못하지만 또다른 차원의 필요성을 느낀다는
http://www.youtube.com/watch?v=2Snoepcmi9U
이렇게 빌과 테드가지고 쭉 transformation과 동차좌표계에 대한 이야기를 끌고 가네요....
그다음....시리즈로 쭉 있습니다......일단 위의 2개만 보았는데요....
'예전 > 3D' 카테고리의 다른 글
| 모델변환과 시점변환 (0) | 2014.12.09 |
|---|---|
| 어파인 공간 (0) | 2014.12.09 |
| 동차좌표 (0) | 2014.12.05 |
| D3D11 wireframe (0) | 2014.05.23 |
| Direct3D의 그리기 2. 정점 버퍼 (0) | 2014.04.06 |
